Le défi
Voici un petit challenge : écrire un script Python qui calcule la somme de tous les nombres premiers compris entre 1 et n = 100.
Un bon test pour voir ce que l’IA peut faire ? Voyons voir !
Claude Sonnet 4.5
Première tentative avec Claude. Voici sa réponse :
def is_prime(n):
"""Check if a number is prime."""
if n < 2:
return False
if n == 2:
return True
if n % 2 == 0:
return False
# Check odd divisors up to sqrt(n)
for i in range(3, int(n**0.5) + 1, 2):
if n % i == 0:
return False
return True
# Find and sum all prime numbers between 1 and 100
prime_sum = 0
primes = []
for num in range(1, 101):
if is_prime(num):
primes.append(num)
prime_sum += num
print(f"Prime numbers between 1 and 100: {primes}")
print(f"Sum of all primes: {prime_sum}")Claude a créé une fonction détaillée avec des commentaires, qui fonctionne et nous donne le résultat suivant:
Prime numbers between 1 and 100: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
Sum of all primes: 1060L’approche proposée par Claude consiste à scinder le problème en deux étapes: créer une fonction indicatrice qui renvoie True si un nombre est premier, False sinon, et utiliser cette fonction pour ne sommer que les nombres premiers parmi les entiers compris entre 1 et n = 100.
Mistral AI
Faisons maintenant le test avec Mistral AI. Voici la réponse du Chat:
def is_prime(n):
if n <= 1:
return False
for i in range(2, int(n**0.5) + 1):
if n % i == 0:
return False
return True
sum_primes = sum(num for num in range(2, 101) if is_prime(num))
print("Sum of primes between 1 and 100:", sum_primes)Deux salles, deux ambiances : ici le code est succinct et va droit au but ! Le résultat est identique:
Sum of primes between 1 and 100: 1060L’approche utilisée par Le Chat est identique à celle de Claude (une indicatrice puis une somme). Observons toutefois qu’ici Le Chat ne traite que le cas particulier n <=1, et utilise une ‘list comprehension’ assez pythonique pour exprimer la somme. Elégant !
qwen/qwen3-4b
Qu’ont en commun Claude et Le Chat ? Le modèle tourne sur leurs serveurs, nécessitant l’envoi de nos données sur ces-dits serveurs. Peut-on tourner un modèle LLM en local ? Eh bien oui, à condition d’avoir des capacités de calcul élevées, du temps devant soi, ou de choisir un plus petit modèle comme qwen/qwen3-4b (utilisé via LM Studio). Voici sa réponse:
def is_prime(n):
if n <= 1:
return False
if n == 2:
return True
if n % 2 == 0:
return False
for i in range(3, int(n**0.5) + 1, 2):
if n % i == 0:
return False
return True
# Sum all prime numbers between 1 and 100
prime_sum = sum(n for n in range(1, 101) if is_prime(n))
print("Sum of prime numbers between 1 and 100:", prime_sum)Une réponse qui a mis un peu de temps à arriver, mais qui en plus de ne pas envoyer les données dans les nuages et d’être peu onéreuse est en ligne avec leurs précédentes approches et donne le résultat suivant:
Sum of prime numbers between 1 and 100: 1060Quid de la performance si n augmente ?
Le challenge de départ consistait à sommer les nombres entiers premiers compris entre 1 et n = 100. Comme nous l’avons vu, les trois modèles de langage ont retourné un algorithme qui fonctionne et donne le résultat rapidement, n étant petit.
Que se passe-t-il si l’on souhaite maintenant sommer les nombres premiers compris entre 1 et n = 1’000 ? ou n = 10’000 ? On s’attend à ce que l’ordinateur mette plus de temps, mais combien exactement ?
Pour cela, écrivons un petit programme qui mesure le temps de calcul de chacun des trois algorithmes (on imagine que le temps va être identique mais pour la forme) pour différentes valeurs de n.
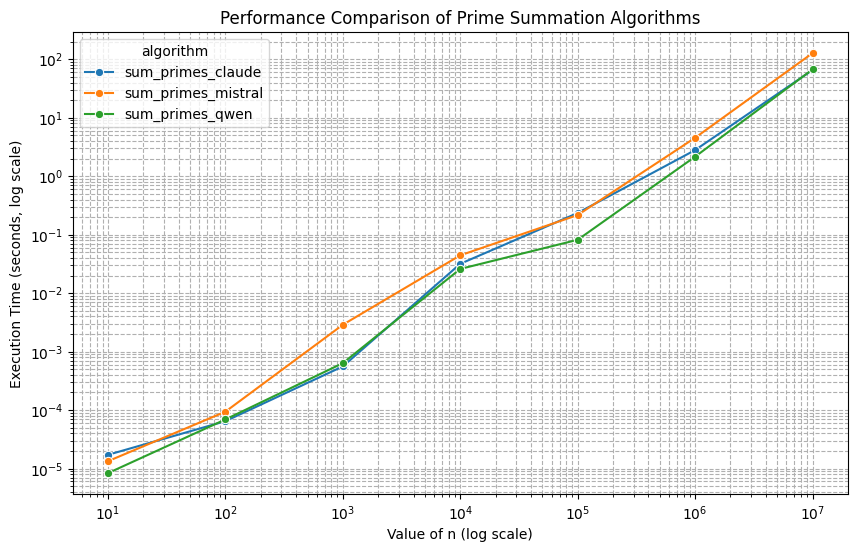
Retour 2300 ans en arrière
Nous sommes en 2025 et tout le monde parle de l’IA. Mais il y a 2’300 ans environ, on parlait déjà de nombres premiers, en particulier Eratostène qui a travaillé sur l’identification de tous les nombres premiers jusqu’à n (tiens, tiens), et y a apporté sa contribution en développant une technique d’exclusion appelée crible d’Eratostène.
Voulez-vous essayer de deviner comment fonctionne cette technique ?
Plutôt que de tester chaque nombre entre 2 et la racine carrée de n, Eratostène va faire l’hypothèse que chaque entier jusque n est premier, puis éliminer les multiples de ces nombres premiers. Par exemple 2 est premier, et on va éliminer tous ses multiples à partir de son carré, soit 4, 6, 8, etc. De même pour 3, on élimine 9, 12, 15, etc. Cette approche par élimination est plus rapide car elle évite de tester des candidats dont on sait par avance qu’ils ne seront pas premiers (car multiples de nombres premiers).
Mais alors si on diminue le nombre de candidats à tester… l’algorithme va plus vite ? Faisons le test !
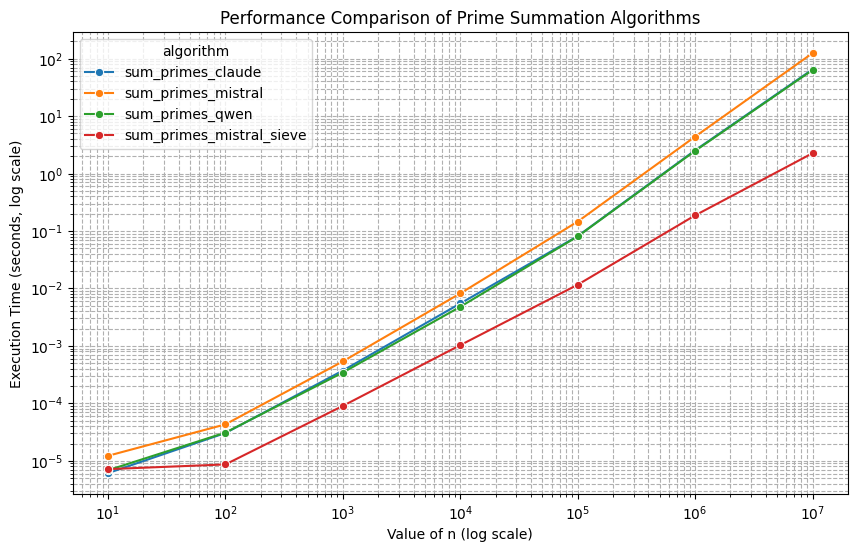
Conclusion
En présentant le même problème à différents modèles, nous avons comparé leurs approches et observé ceci:
- globalement tous les modèles retournent le même algorithme, reflétant probablement des modes et sources d’entraînement très similaires
- sur un problème assez “simple”, un petit modèle n’a pas à rougir et rivalise avec les grands, certes en prenant son temps, mais à moindre coût et en gardant les données en local
- aucun modèle parmi ceux testés n’a inclus le crible d’Eratostène dans son algorithme, peut-être pour garder un code simple, peut-être pour réserver cette technique à des prompts plus spécifiques
En conclusion, cela peut sembler assez magique de donner un problème à un ordinateur et obtenir une solution immédiate. Un regard critique et curieux sur cette solution n’est toutefois pas superflu, que ce soit pour s’assurer qu’elle fonctionne, ou qu’il n’en existe pas de meilleure.